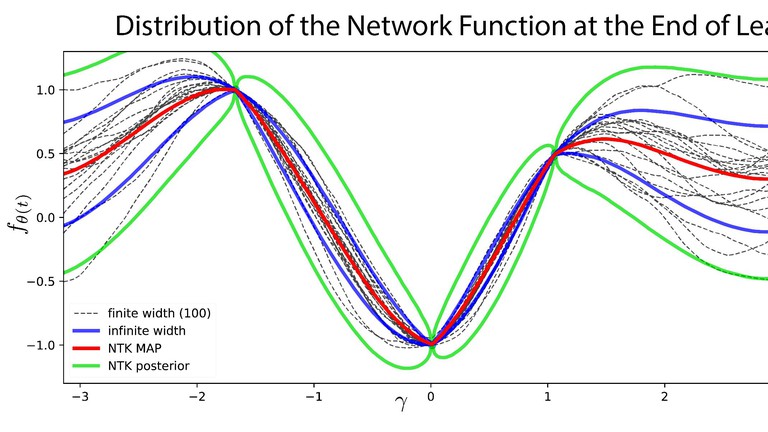
Institut de Mathématiques – MATH

Contact
Director
Pour toutes questions sur l’enseignement merci de consulter les pages SMA ci-dessous : https://www.epfl.ch/schools/sb/sma/fr/contacts-et-organisation/
Mailing Address
Institute of Mathematics
EPFL SB MATH
MA A2 383 (Bâtiment MA)
Station 8
CH-1015 Lausanne
Switzerland